Move is a verification-friendly programming language that enables users to specify and formally verify smart contracts. In a previous post I explained how to specify and verify conditions under which a function aborts.
In this post, we focus on the verification of programs with loops. Formally verifying programs with loops is non-trivial, because loops may execute an arbitrary and unbounded number of times, making it hard to reason about their behaviors in all possible cases.
A simple motivating example
Here’s a typical implementation of a function that scans a list xs of type vector, where E is the generic type of the elements in the list, to check if it contains an element e:
module 0x02::Contains {
/// Return true if and only if the element `e` is in the list `xs`.
fun contains<E>(xs: &vector<E>, e: &E): bool {
let i = 0;
while (i < xs.length()) {
if (xs.borrow(i) == e) {
return true;
};
i = i + 1;
};
// If we are here we have not found the element and i == len(x)
return false
}
}Figure 1: The function contains computes whether the list xs contains an occurrence of an element e. I have adopted the Move 2 receiver-style function syntax and used xs.length() instead of the more verbose vector::length(xs).
The correct behavior of this program can be specified by:
SpecContains: The result (of type
bool) returned by this function istrueif and only if, there is an indexisuch thatxs[i]is equal toe.
However, is this specification sufficient? Unfortunately no, because loops may not always terminate. But loop verification is an old problem and there are well-established techniques to address this challenge:
(Loop) termination proof: Demonstrating that a loop always terminates by defining a ranking function i.e., a measure that strictly decreases with each iteration and takes its values in a well-founded set.
Loop invariants: Establishing an inductive property that remains true throughout the loop’s body successive executions, ensuring correctness over an arbitrary (but finite) number of iterations.
When combined, these techniques help verify both the correctness and termination of loops, ensuring that the function always terminates and behaves as intended in all cases.
Loop termination is a critical topic; however, the Move Specification language does not include a built-in mechanism for proving termination. In this post, we will not be addressing proof of termination.
It’s important to note that while programs in the MoveVM are constrained to terminate due to gas limits, this does not render loop termination irrelevant. If a loop is written with unintended edge cases or bugs that prevent it from terminating, it will eventually trigger an out-of-gas exception, rather than yielding the expected result. This is problematic if the computation is expected to complete successfully.
In this post, we explain what loop invariants are, how they work, and how to use them in Move programs to verify programs with loops.
Why is this important?
Smart contracts on blockchain platforms (such as Ethereum, Move, Solana, etc) rely on efficient on-chain data structures — such as (Hash)Maps, Sets, Vectors, and Merkle Trees — to manage the chain state, store assets, and process transactions. These structures often require looping constructs to iterate over data. Bugs in loop-based processing can lead to asset loss, contract failures, or broken business logic.
Loops are hard to reason about and prone to subtle errors. Additionally, loops are computationally expensive (e.g., gas costs in Web3), leading developers to optimize them, often at the risk of introducing unintended bugs.
This is why rigorous analysis and formal verification of loops are essential to ensure correctness, security, and efficiency of smart contracts.
Background
To formally prove that the while-loop in Figure 1 behaves as intended, we rely on two key concepts:
Specification: A formal definition, using logical predicates of the program’s intended behavior.
Instrumentation: The addition of proof hints, such as loop invariants, that guide the Move Prover in verifying the correctness of the program.
Specification
Let's start with a specification for the function contains: what does it mean that e is contained in xs? It means that there is an index i, such that xs[i] = e. We can write our specification "there is an index i, such that xs[i] = e" as a logical predicate using the exists quantifier: ∃isuch that: 0≤i<|xs|and xs[i]=e. The Move Specification Language supports quantifiers, and to add a formal specification to our code, we write a spec for contains:
spec contains {
// It never aborts.
aborts_if false;
// SpecContains
ensures result // same as `result == true`
<==> // if and only if
(exists i: u64 where 0 <= i && i < len(xs): xs[i] == e);
pragma unroll = 50;
}The variable result (of type bool) in the specification stands for the value returned by the function. If we run the the Move Prover on this code, it is unable to verify that the post-condition specified in the ensures in SpecContains holds (but the Prover succeeded in proving that the function does not abort, which is already good progress!).
git:(master) ✗ aptos move prove -f contains
[INFO] preparing module 0x2::Contains
[INFO] transforming bytecode
[INFO] generating verification conditions
[INFO] 1 verification conditions
[INFO] running solver
[INFO] 0.21s build, 0.01s trafo, 0.01s gen, 0.70s verify, total 0.94s
error: post-condition does not hold
┌─ .../move/move-learning/use_assert/sources/contains.move:20:9
│
20 │ ╭ ensures result // same as `result == true`
21 │ │ <==> // if and only if
22 │ │ (exists i: u64 where 0 <= i && i < len(xs): xs[i] == e);
│ ╰────────────────────────────────────────────────────────────────────────^
│
...
{
"Error": "Move Prover failed: exiting with verification errors"
}The message "error: post-condition does not hold" (line 8) may sometimes be misleading. Indeed, we'll be able to prove that the post-condition holds later by adding loop invariants. A more accurate message in this case is "post-condition may not hold" which indicates that the Prover was not able to prove it holds.
To understand why the Prover cannot prove SpecContains, it may be useful to understand how loops are treated by the Move Prover.
Abstract effect of a loop
The Move Prover treats a loop almost as a black box, meaning it does not track the loop’s internal effects in detail. Instead, the loop effect is abstracted away, which can make it difficult to reason about its behavior in proofs.
To track useful (proof) information in a loop, we need to instrument it with predicates and derive a post-condition that holds after the loop terminates. On way to achieve this is to add a (candidate) loop invariant to the code. This requires guessing a predicate, the loop invariant, and then verifying that it is indeed preserved by the loop.
If the loop is executed a finite and small number of times, we can also unroll the loop. This approach is faster and does not require finding a loop invariant, but it only works for loops with a bounded (and small) number of iterations.
We review the two options in the rest of this article starting with loop unrolling.
Proving programs with loops
Loop unrolling
Loop unrolling can be enabled in specifications using a pragma in the Move Specification Language. The following example (line 23) illustrates how to apply it:
spec contains {
// It never aborts.
aborts_if false;
// SpecContains
ensures result // same for result == true
<==> // if and only in
(exists i: u64 where 0 <= i && i < len(xs): xs[i] == e);
pragma unroll = 50;
}With this pragma, the Prover unrolls the loop for up to 50 iterations. Unrolling means that it expands the loop body sequentially up to the given limit, effectively simulating execution for up to 50 iterations. We can think of unrolling as manually expanding the loop as follows:
let i = 0;
// first iteration
if (i < vector::length(x)) {
if (vector::borrow(x, i) == e) {
return true;
};
i = i + 1;
} else {
return false
}
...
...
// 50-th iteration
if (i < vector::length(x)) {
if (vector::borrow(x, i) == e) {
return true;
};
i = i + 1;
} else {
return false
}
/// if we are here we consider the program is correct as we have
/// unfolded the loop 50 times.Loop unrolling ignores cases where the loop runs beyond the limit, and the Prover does not issue a warning that a bound for loop unrolling was used.
As you can imagine, this approach quickly becomes intractable. Expanding the loop body multiple times can significantly increase the complexity of the underlying logical statement that the Prover (more precisely, its backend Z3) has to verify, leading to excessive memory and time consumption, and ultimately exhausting the Prover’s resources.
The graph in Figure 2 illustrates how verification time scales with increasing loop unrolling bounds.
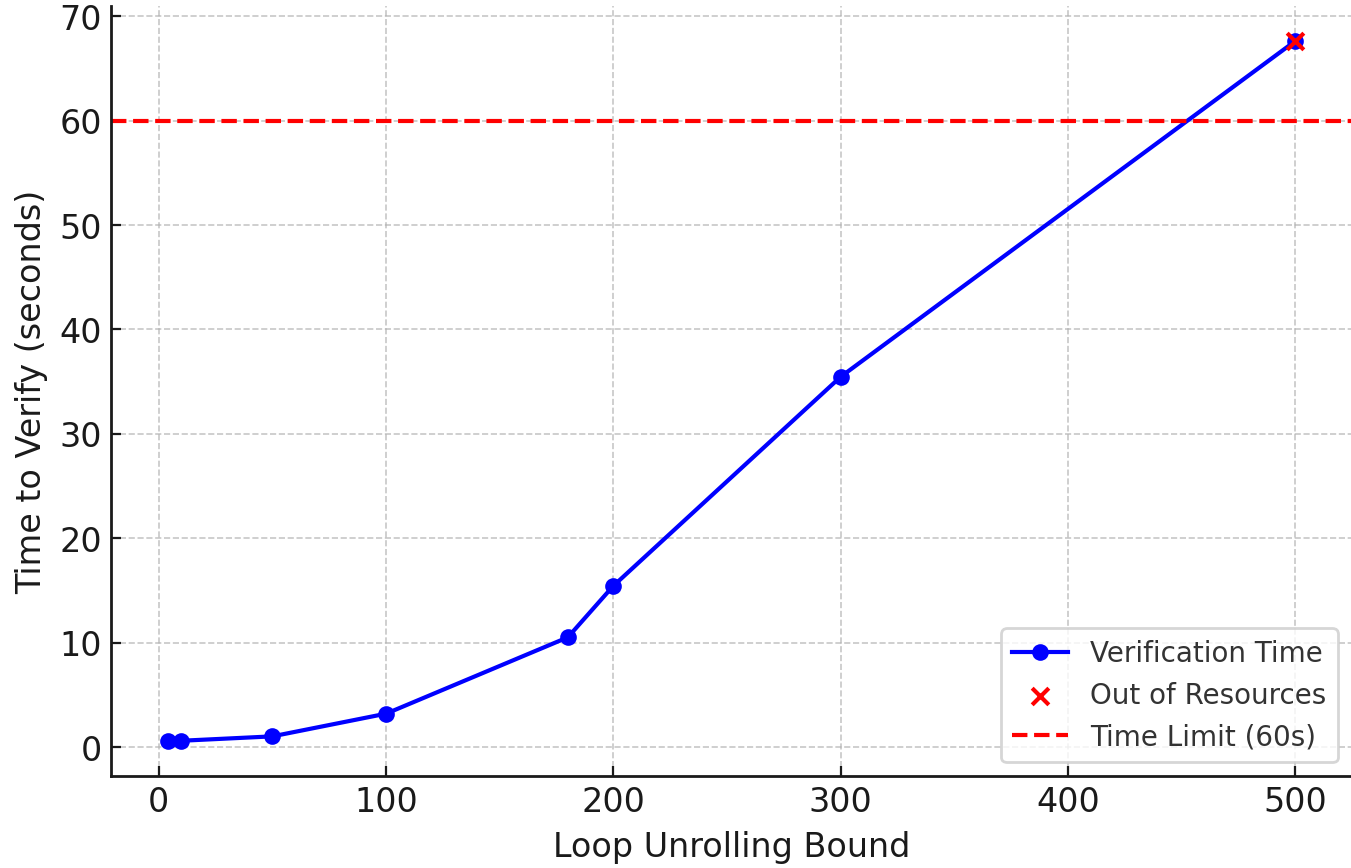
Figure 2: Time to verify contains (in seconds) vs maximum number of loop unrolling.
Loop unrolling is an efficient technique but is practically limited to a small number of iterations and, more importantly, is incomplete. For example, if a function optimizes computation when the vector length exceeds 1000, unrolling the loop fewer than 1000 times will never exercise the optimized code path, leaving it unverified.
Loop unrolling is useful for testing loops. It is easy to enable in Move, does not require discovering loop invariants, and is highly effective for finding bugs. However, it does not guarantee the absence of bugs beyond the unrolling limit.
Loop invariants address this limitation by providing a generalized proof that holds for any number of iterations, ensuring correctness beyond a fixed unrolling bound.
Loop invariants
What are loop invariants really? How do they work? In this section we explain how loop invariants can be proved by induction.
We illustrate the technique with a simple program and then apply it to our Move function contains in the following section.
An inductive invariant for a loop is a predicate that:
holds on entry, before the first iteration of the loop,
is preserved by the executing the loop body.
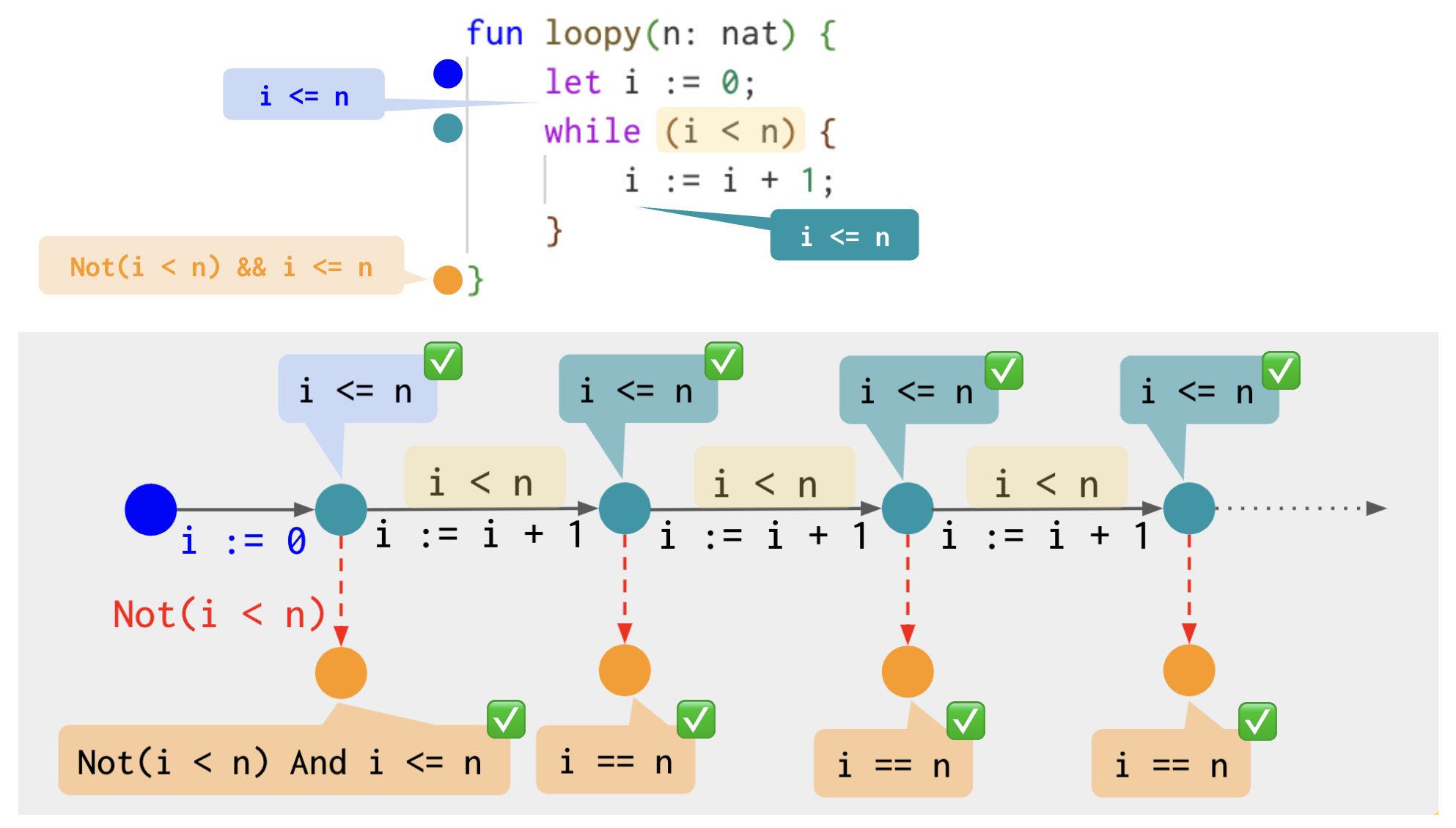
Figure 3: The transitions (arrows) read as follows: if the condition on the top of the arrow (e.g. i < n) is satisfied then the update (e.g. i := i + 1) below the arrow is performed. The predicate i <= n is a loop invariant, and this can be proved by induction, it is an inductive invariant. This loop invariant can be used to obtain a post-condition for the loop i == n.
In Figure 3, we have a simple program with a while loop, with nat the type for natural numbers, i.e. non-negative integers. The colored dots , , and , on the left are control locations of the program, i.e. point to what instruction/control structure is executed next. Let's test a few candidate predicates, and see whether they satisfy the loop invariant conditions (1) and (2) given above:
i < n: this predicate does not hold at after we executevar i := 0ifnis zero. It does not hold on entry and is not a loop invariant.now assume we require
n >= 1when callingLoopy. So at we haven >= 1. Isi < na loop invariant? No because if we start withi < nand we incrementi(execute the body of the loop), we don't necessarily end up withi < n. A counter-example is to start withi == n - 1.what about
i <= n?. Yes it is an invariant and we explain hereafter how to prove it.
First i <= n holds on entry to the loop at after we execute var i := 0 and this for any input value n: nat. Second, is the predicate i <= n preserved by the loop body? Yes, but how can we prove it?
Assume we start with a given value i_0 for i and i_0 <= n and we execute the loop body, starting at . If we enter the loop, the condition of the loop i < n must be satisfied, so i_0 < n holds. The effect of the loop body is to increment i, so the new value i_1 of i after executing the loop body is i_1 == i_0 + 1. Is i_1 <= n? Yes because i_0 < n, and i_1 == i_0 + 1 <= n.
The execution of the loop follows the pattern described in Figure 3:
1. start at control location . If the current value of i is such that i < n then execute the loop body i := i + 1 and go to control location (loop).
2. if i >= n then exit the loop and go to control location .
As we have established that i <= n is a loop invariant we know:
it holds on entry at after executing the code at BLUE,
every time we iterate the loop → → … → , it is preserved, so by induction, it holds after each iteration of the loop.
it also holds at when we exit the loop (provided the condition of the loop does not have side-effects, which is the case here).
As a result we can conclude that whenever the loop terminates, we reach control location and the loop invariant i <= n holds. We also know that if we exit the loop, then the loop condition is false and i >= n holds, and combining the two predicates yields i == n.
The proof above (using i_0 andi_1) is exactly what automated verification tools do (with the help of a backend SMT-solver) to check whether a candidate predicate is indeed a loop invariant.
Loop invariants in Move
We can now try to find a good loop invariant for the code in Figure 1. We want our loop invariant to be good enough to be able to prove the post-condition of contains which is result <==> (exists i: u64 where 0 <= i && i < len(xs): xs[i] == e). So ideally when combining our loop invariant with the exit condition of the loop, it implies our post-condition. If we look carefully at the loop, we can see that the loop terminates (exits) in two cases:
i < xs.length()(withreturn) and this happens when we have just found a matchxs[i] == e.i == xs.length()(exit the loop), and this should indicate thateis not inxs.
So what would be a good candidate loop invariant? Unfortunately there is no magic recipe to find good loop invariants. There are some stratregies that can help to find invariants in practice. So here is how I have approached the proof of contains.
1. the post-condition is an if and only if. What I first do is to split it into two ifs:
(a) result ==> (exists i: u64 where 0 <= i && i < len(xs): xs[i] == e)and
(b) (exists i: u64 where 0 <= i && i < len(xs): xs[i] == e) ==> result Then run the Move Prover. If we do this, we can see that the Prover can automatically (with no need for a loop invariant) prove (a). So if we need a loop invariant, it is for proving the remaining case (b).
2. let's focus on proving (b). We can add a candidate invariants as per line~9 in the code below: this candidate specifies that all the values we have scanned so far (j < i) do not match e. If we run the Prover, it is now able to prove that our candidate invariants is indeed an invariant, and also the prove the <==>condition at line~28.
module 0x02::Contains {
/// Return true if and only if the element `e` is in the list `xs`.
fun contains<E>(xs: &vector<E>, e: &E): bool {
let i = 0;
while ({
spec {
invariant i <= len(xs);
invariant (forall j: u64 where 0 <= j && j < i: xs[j] != e);
};
i < xs.length()
}) {
if (xs.borrow(i) == e) {
return true;
};
i = i + 1;
};
// If we are here we have not found the element and i == len(x)
return false
}
spec contains {
// Never aborts
aborts_if false;
// SpecContains
ensures result // same as result == true
<==> // if and only if
(exists i: u64 where 0 <= i && i < len(xs): xs[i] == e);
}
}Finding good invariants is an art, and may require experience. But modern tools like AI coding assistants can suggest invariants. This is a safe way of using an AI coding assistant as the proposed invariant is checked by the Prover, so if it is wrong the Prover will flag it. If you find it hard to guess a loop invariant you can ask a coding assistant to help you.
Simple guidelines for proving programs with loops
When verifying programs that contain loops, a structured approach helps simplify proofs and identify potential bugs. The following steps provide a practical strategy for handling loops in formal verification:
Start with loop unrolling. This helps to quickly identify issues in simple cases before dealing with invariants. If unrolling fails, it may indicate incorrect assumptions or missing constraints in the specification.
Propose a loop Invariant (General Proof). Once you have been able to prove the specification for a bounded number of iterations, try to find a good loop invariant.
Break down complex proofs if necessary. For example, if proving an if-and-only-if (
A <==> B) specifications split them into two separate implications. ProveA ==> BandB ==> Aseparately. This technique helps isolate independent conditions, making each proof step easier.Try candidate invariants. As the Prover is going to check that the predicates you propose as
invariantare indeed loop invariants, it is easy to try candidates and see if they are correct.
Summary: A structured approach to loop verification
Use loop unrolling to test simple cases.
Find a loop invariant to handle general cases.
Split complex proofs (e.g., if-and-only-if) into simpler conditions.
Prove each condition separately to simplify the identification of the invariants.
This method balances quick testing, formal verification, and logical decomposition, making it easier to prove correctness properties of programs with loops.

