Rollups or Layer 2s (L2s) are scaling solutions to extend a Layer 1 (L1, e.g. Ethereum) that provides strong security guarantees. There are currently two dominant types of rollups, validity (ZK-proof) and optimistic (fraud proof) rollups. Both use an L1 for settlement, i.e. the confirmation of irreversibility (or immutability) of a transaction. Settlement time is still a problem for both types of rollups: for a ZK-rollup (ZK-RU) it is in the order of half an hour, whereas for optimistic rollups (OP-RU) it is in the order of days (typically 7). This can be a limiting factor for certain types of DeFi applications (e.g. arbitrage).

At Movement Labs, we are developing the next generation of L2s, with an execution layer powered by the high-throughput Move Virtual Machine (MoveVM) and smart contracts written in Move, a programming language offering strong security guarantees (e.g. re-entrancy is not allowed) and leveraging formal verification techniques.

While the Movement Network is designed to support optimistic mechanisms, we strive to offer our users choices for settlement depending on their needs. This ranges from optimistic (fraud proof), to validity (zk-proof), to a new fast-finality mechanism (in the order of seconds), and to various hybrid versions of these (zk-fraud proof, fast-finality with fraud proof).

In this post, we introduce our fast-finality mechanism. We start by defining Ethereum's security and then compare the security, latency, and complexity levels of different types of settlement mechanisms, optimistic, validity, and our own fast-finality to help users decide what is best for their target applications.

TL;DR

The highest level of security is provided by ZK-rollup, but the correct implementation (satisfying the ZK-trust assumptions) is complex (risks of bugs). Optimistic rollups are easier to implement, but there is a risk of invalid blocks, and they rely on a correct implementation of the dispute resolution mechanism, which is not trivial. Soft-finality, i.e. when the rollup has generated a block, is not secured in ZK-RU and OP-RU.

Fast-finality settlement (FFS) is simple enough to implement (so you can have high confidence in the implementation). In FFS, Soft-finality is secured by the L2 validators' stakes, which provides a minimum level of security. It is more secure than OP-RU and faster than ZK-RU.

The table below summarizes the types of settlement and their properties:

The Movement Network offers the choice of settlement mechanism for each chain in the network. Depending on their applications, users can decide what configuration they want to adopt to meet their needs.

Ethereum Security

We first define Ethereum's security and finality. You may have heard or read this several times:

Our chain/protocol/rollup inherits Ethereum security.

What does that mean? And how is security defined and quantified on Ethereum? How does it transfer to (or how is it inherited by) another component?

As we are interested in quantifying security (on Ethereum), we are going to abstract away some of the implementation details that are not relevant for this discussion.

The Abstract Model

Users submit transactions to the nodes in the (Ethereum) network. The nodes in the network build blocks. Each block 𝐵 is a triple (𝐵.𝑠𝑡, 𝐵.𝜎, 𝐵.𝑝𝑎𝑟𝑒𝑛𝑡) with:

• B.parent is a reference to the parent block of B.

• B.st is state. This is a mapping form users to their assets, and for contracts to their current states.

• 𝐵.𝜎 is a sequence of transactions.

The genesis block 𝐺 = (𝜄, [], ⊥) is the block defined by the initial state of the system 𝜄, the empty list of transactions [], and no parent block which is denoted by ⊥.

There are reference semantics that define the state transition function. This function maps pairs (state, sequence of transactions) to states, and we write

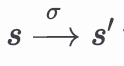
for: from state 𝑠, executing the sequence of transactions 𝜎 leads to state 𝑠′. These semantics are implemented in the Ethereum Virtual Machine (EVM).

Given a block 𝐵, 𝑐ℎ𝑎𝑖𝑛 (𝐵) is the chain defined by recursively collecting the parent blocks of 𝐵. We assume 𝑐ℎ𝑎𝑖𝑛(𝐵) is always well-founded (finite and no cycles) and ends up in the genesis block. Given a block 𝐵 and chain(B)=B_k-1...B₀ with B_k = B and B₀ = G, chain(B) is valid if

the sequence of states computed since the genesis block satisfy the reference state transition semantics. (note: this definition implies that the genesis block is valid and the only chain of length 1 that is valid is the genesis block.)

If chain(B) is valid, we simply say that B is valid.

Proof of Stake & Finality

The consensus protocol used in Ethereum is a Proof of Stake (PoS) protocol. In Ethereum PoS, a set of nodes called validators each stake the same amount, 32ETH. The role of the validators is to determine which blocks are valid. To do so they have to attest for blocks. An honest validator attests only for valid blocks. A dishonest (Byzantine) validator can attest for non-valid blocks, many different sibling blocks, or tamper with messages (within some limitations, e.g. they cannot forge signatures). Dishonest validators can have their stake slashed if they are caught misbehaving, and honest nodes are rewarded for their good work. This mechanism incentivizes nodes to be honest.

At a (very) high-level, validators attest for blocks. When more than 2/3 of the validators have attested for a block, a block becomes finalized (in the real network, this is more complicated, as blocks at checkpoints go through different states, justified, finalized). A transaction is finalized (confirmed and irreversible) when it is included in a finalized block.

Under the assumption that less than 1/3 of the validators can be Byzantine, every finalized block is valid.

Indeed, if a block 𝐵 is finalized, more than 2/3 of the validators have attested for it. In this 2/3 there must be at least one honest validator (as less than 1/3 can be Byzantine). An honest validator only attests for 𝐵 if 𝐵 is valid, so 𝐵 is valid. QED.

Security

The Ethereum network is secure if each finalized block is valid.

Under the previous assumption that at most 1/3 of the validators can be Byzantine, the PoS protocol ensures the network is secure.

But when is this assumption realistic?

To produce an invalid finalized block, more than 2/3 of the validators must attest for it. A validator can be intentionally dishonest or unintentionally (because of a bug, or using the wrong version of the reference semantics). Let's assume that there is no unintentional dishonest validator.

Assume an attacker wants to produce an invalid finalized block 𝐵, then they have to control or convince more than 2/3 of the validators to attest for it. If they only want to prevent reaching consensus (liveness), they need to control or convince 1/3 of the validators to misbehave. To control a validator, an attacker must have staked/spent 32ETH. So, assume there are 𝑉 validators, each of them staking 32ETH. The total stake (in ETH) is 𝑆 = 32 × 𝑉, and an attacker needs at least 1/3 ∗ 𝑆 (resp. 2/3) to compromise the liveness (resp. security) of the network (we assume here that there is no network partition).

As of today there are more than 1,000,000 validators operating in the Ethereum network. To control 1/3 of the validators, it would take an attacker to invest more than 1/3 × 1,000,000 × 32 × 2,800 ≈ 29,000,000 ,000 USD, close to 30 Billion, and close to 60 Billion to finalize an incorrect block.

It is very unlikely that an attacker (there is only one Elon Musk) would be able or willing to invest such a huge amount of resources. Moreover, to stake this amount would take months due to the rules in place to join and exit the validators set.

Security is about probability. If the probability of an attack is 𝜀 we can define the security level as 1 − 𝜀. The network is secure if 𝜀 is small or negligible.

The likelihood of an attack decreases when the total stake increases, and when the total stake is very large, it becomes negligible. In that case, we can say that the "at most 1/3 Byzantine" assumption is realistic and the network is secure. The level of security of Ethereum (with the current total stake) is referred to as Ethereum's security.

This notion of security is different to the notion of security for smart contracts, which is the absence of bugs. The fact that Ethereum is secure does not rule out bugs that could lead to unintended results (e.g. re-entrancy attacks). In the security analysis above, we assume that if the code of a contract is executed according to the reference semantics (of the EVM), the resulting block is valid.

Security of Validity and Optimistic Rollups

A rollup is an L2 with settlement on L1 (usually Ethereum). What is that? It means that the L2 computes the next L2-block and provides some data to the L1 to verify that this block is valid.

The definitions of valid block/chain for an L2 are similar to the definitions given previously for Ethereum.

Validity (ZK) Rollup

In a ZK-rollup, the L2 provides a ZK proof of validity of blocks to the L1. The proof 𝜋(𝐵) for block 𝐵 is built by a prover and is supposed to prove the statement "Block 𝐵 is valid". This proof is checked by a Verifier, a contract on L1.

ZK-Trust Assumptions. We assume that the machinery to build the proof (zk/crypto libraries) and the Prover (ZK-VM) is bug-free and:

• ZK-A1) the Prover is correct and generates a proof 𝜋(𝐵) that is accepted by the Verifier if and only if 𝐵 is valid.

• ZK-A2) the probability that the Verifier accepts an incorrect proof is negligible.

• Zk-A3) the implementation of the Verifier, VerifierK, which is a contract on L1 that verifies the proof, correctly implements the Verifier algorithm.

An L2-block 𝐵 is finalized when the verifier contract has accepted the proof. This verification step is an L1 transaction and on Ethereum takes approximately 12 minutes (two epochs) to be finalized.

What is the security level of a ZK-rollup? Under the ZK-trust assumptions above, an attacker needs to control 1/3 of the validators to prevent the VerifierK transaction to be finalised. An attacker needs to control 2/3 of the Ethereum validators to tamper with the result of the VerifierK contract and to finalize an invalid L2-block.

A ZK-rollup has the same security as Ethereum and inherits Ethereum's security. Time-wise finalization takes on average 20 minutes (time to generate a proof) plus finalization on L1, 12 minutes. Overall in the order of 30 minutes.

Optimistic Rollup

In an optimistic rollup, a block 𝐵 is finalized if it has not been successfully demonstrated invalid within a challenge period. For instance, assume block 𝐵 is produced by the rollup. If after the challenge period (7 days) it has not been disputed, then it becomes final (even it is not valid). If it is disputed and a third-party claims that instead of 𝐵 we should have 𝐵′, then a dispute resolution mechanism is triggered to decide between 𝐵 and 𝐵′.

OP-Trust Assumptions. We assume that:

• OP-A1) the fraud proof service (e.g. bisection algorithm) is correct. When submitted two different blocks 𝐵 and 𝐵′ (and assuming one of them is valid), it identifies the valid block.

• OP-A2) the implementation of the fraud proof service is correct.

As mentioned before, the optimistic rollup set up allows invalid blocks to be finalized: an invalid block may not be disputed within the challenge window and become finalized. Under the extra assumption

• OP-A3) that at least one honest validator (watchtower) verifies a block within the challenge window

then an optimistic rollup is secure: it cannot finalize invalid blocks.

Compared to the ZK setting this notion of security is strictly weaker than a ZK rollup, as invalid blocks can be created for free (if no dispute happens). Time-wise the challenge window is in the order of 7 days (plus 12 minutes but this is negligible), and hence finalization is 7 days.

Fast-Finality Settlement

In the previous set ups (ZK or Optimistic rollups), the notion of finalization is binary, yes or no, and this is either decided by an L1 transaction (verification of a proof for zk-rollups) or a timeout for optimistic rollups.

We propose here a protocol that provides fast-finality using a staking mechanism.

When a block is produced by the L2, it is made available to L2 validators. The validators check the validity of the block and attest for it. This provides a first level of finalization (soft-finalization), the security/trust of which is determined by the number of validators that have attested for the block. The stakes of the L2 validators are managed by an L1 contract.

In a fast-finality settlement, we have a set of validators whose role is to quickly check L2-blocks. The validators stake in a contract on L1, the StakingK contract. For the sake of simplicity we assume all the validators stake the same amount, and we refer to the L2-stake for the stake locked in the StakingK contract.

Validators operate L1 full nodes and L2 full nodes at the same time. When an L2-block is produced, the validators check the validity of an L2-block. An honest validator attests for an L2-block only if it is valid. They broadcast their attestations to other validators. When a validator has received attestations for a block from 2/3 of the validators, it sends the list of (signed) attestations to the StakingK contract on L1. The StakingK contract checks that:

• the list of attestations is well-formed: no duplicates, the signatures correspond to validators with a non-zero stake, and

• that 2/3 of the validators (super-majority) have attested for the block.

We omit the details here, but a validator sending a non well-formed list of attestations or a list that does not meet the 2/3 threshold is slashed.

An L2-block is finalized when the StakingK contract has verified the 2/3 super-majority. As this is an L1 transaction, it takes approximately 12 minutes to be finalized. The time for the L2 validators to send their attestations is in the order of seconds.

FFS-Trust Assumptions. We assume that:

FFS-A1) at most 1/3 of the L2 validators can be Byzantine,

FFS-A2) the implementation of the StakingK contract is correct, i.e. it correctly checks the 2/3 super-majority and correctly tracks the stakes of the L2 validators.

Under the FFS-trust assumptions, if a block is finalized then it is valid.

What is the security level of a fast-finality settlement? The actual verification of the validity of an L2-block relies on the L2 validators. The stake on the validity of the L2-block is 2/3 of the validators stake (locked in the StakingK on L1). To create an invalid L2-block an attacker needs to control 2/3 of this total L2 stake. The verification step (similar to the verification of a ZK-proof) that 2/3 of the total stake have attested for a block is an L1 transaction. To corrupt this verification step, an attacker needs to control 2/3 of the Ethereum validators' total stake.

Overall to create an invalid L2-block, an attacker needs to control either 2/3 of the total L2 stake locked in the StakingK contract or 2/3 of the total stake of Ethereum's validators (to tamper with the super-majority check).

The stake in the StakingK is likely to be lower than the total stake of Ethereum's validators. However, fast-finality settlement provides a first level of security determined by the L2 stake. When paired with economically strong retstaking mechanisms it can get close to Ethereum's security.